
Improving recall speed in times tables and other maths facts is an important indicator that this knowledge is being reinforced. By following a well-designed and precisely targeted program of revision to follow on from content instruction, recall speeds can approach and attain automaticity – rapid, effortless recall. This is vital to further mathematical learning because it frees the working memory for the next-level concept. As presented in another article, a wide range of student difficulties in maths can be traced back to earlier concepts being missed, or being insufficiently reinforced.
Cholmsky (2011) explains that, by contrast, revision exercises that are poorly designed or poorly suited to the individual can fail to produce gains in recall speed, or even see speed being lost. Therefore, any learning system should be thoroughly validated across the widest possible range of learners and learning environments.
Maths Invaders from EdAlive is a revision tool using automated Adaptive Learning to individualise content. The basic setup encourages speed (12 mixed questions in 40 seconds) and the website records the time taken to respond to each question, in milliseconds.
Many factors affect response time. The number of digits in an answer is a clear influence. The device being used will also play a role, with a full keyboard with number pad facilitating greater speed than, say, a laptop with only a qwerty number row. It can be expected that keyboard dexterity will improve with practice. This is a useful skill in addition to mental recall, but in the current circumstances the two sources of speed gain cannot be readily differentiated. The device in use can be a further complication because it is not uncommon for students to use different devices at different times. There is also the possibility of many user distractions, but it is thought that these will have little impact on trends supported by sufficient data.
For the current study, only the results for questions with 2-digit answers were examined. In an earlier broad-brush examination, we estimated that average response time improved by 1.1 seconds or 26% from an effort equivalent to 10 half-hour sessions, or roughly 1000 correct answers. Importantly, these gains were made at the same time as an improvement in maths age of around 12 months, meaning the Adaptive Learning system is supplying progressively harder questions.
The present study is a more refined estimate of speed gains, specifically considering individuals who have consistently used the same device for a sustained period of activity over a period of weeks.
Jamshidifarsani et al. (2021) conclude that an exponential decay function best describes speed reduction for an individual learning process. This means that when a new skill is learnt, initial slowness is made up for by rapid early gains. Further speed gains require progressively more practice – in other words, there is the widely-observed “diminishing returns” phenomenon.
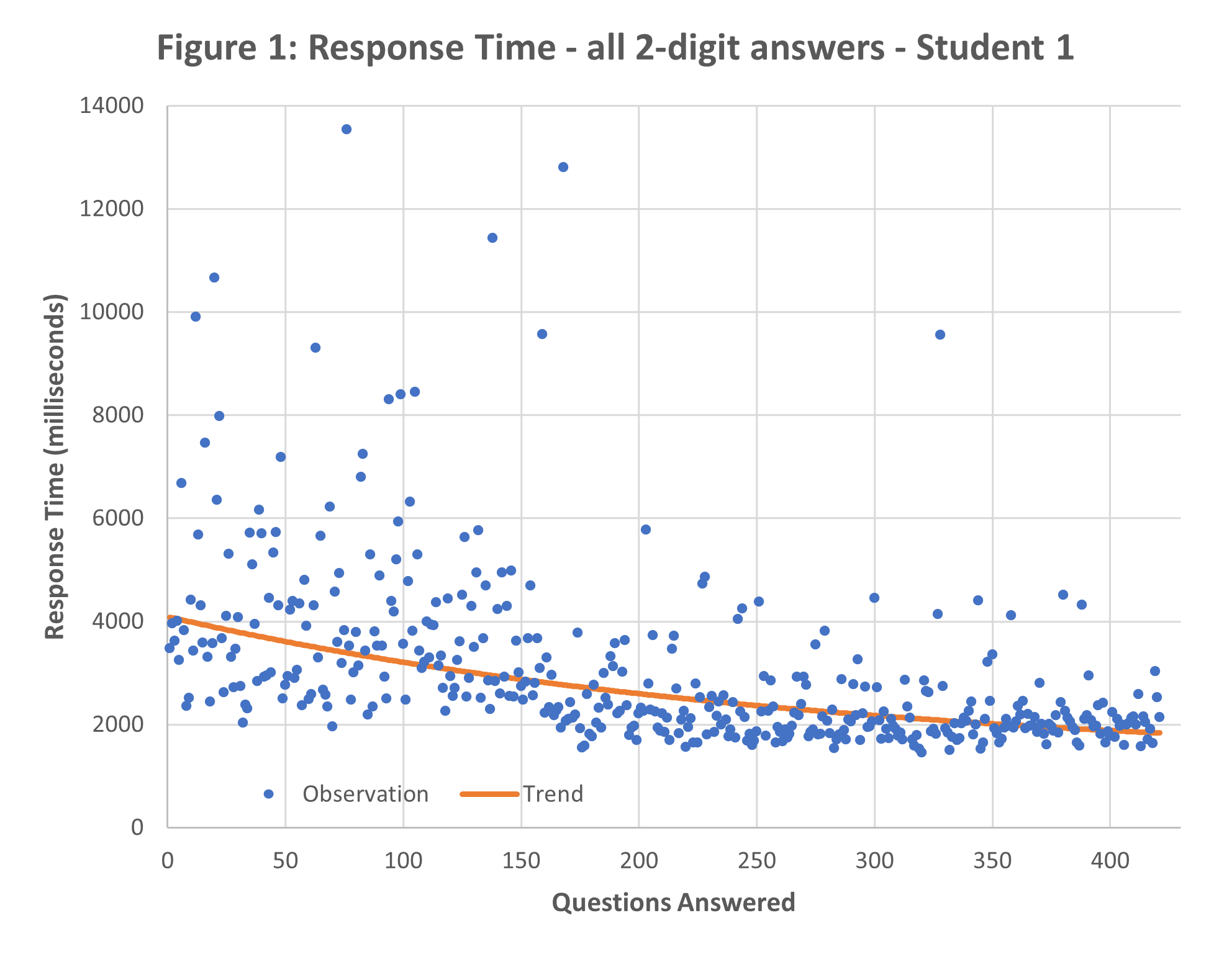
The performance of the first student selected is shown in Figure 1. The response time for each of 421 2-digit correct answers are shown in blue, and the fitted curve in orange. The trend in response times improves from 4.1 seconds to 1.8 seconds, a reduction of 2.3 seconds or 55%. It may be observed that response times around 2 seconds are rare in the early usage, but are consistently achieved in later efforts. By contrast, times exceeding 5 seconds are initially common but become very rare. This means that while there are modest gains in the best times achieved, the majority of progress is through consistency in rapid response.
Further students were similarly examined, and Figure 2 shows the individual trend lines. Clearly, students have different starting points, but in all cases the progress was very strong. All students reduced their average response time by 2.3 to 2.4 seconds, or 42-48%. All students completed this effort over the course of several weeks, so it is highly unlikely that speed gains could be attributed to other sources of maths instruction, as might be possible with a longer time-frame.
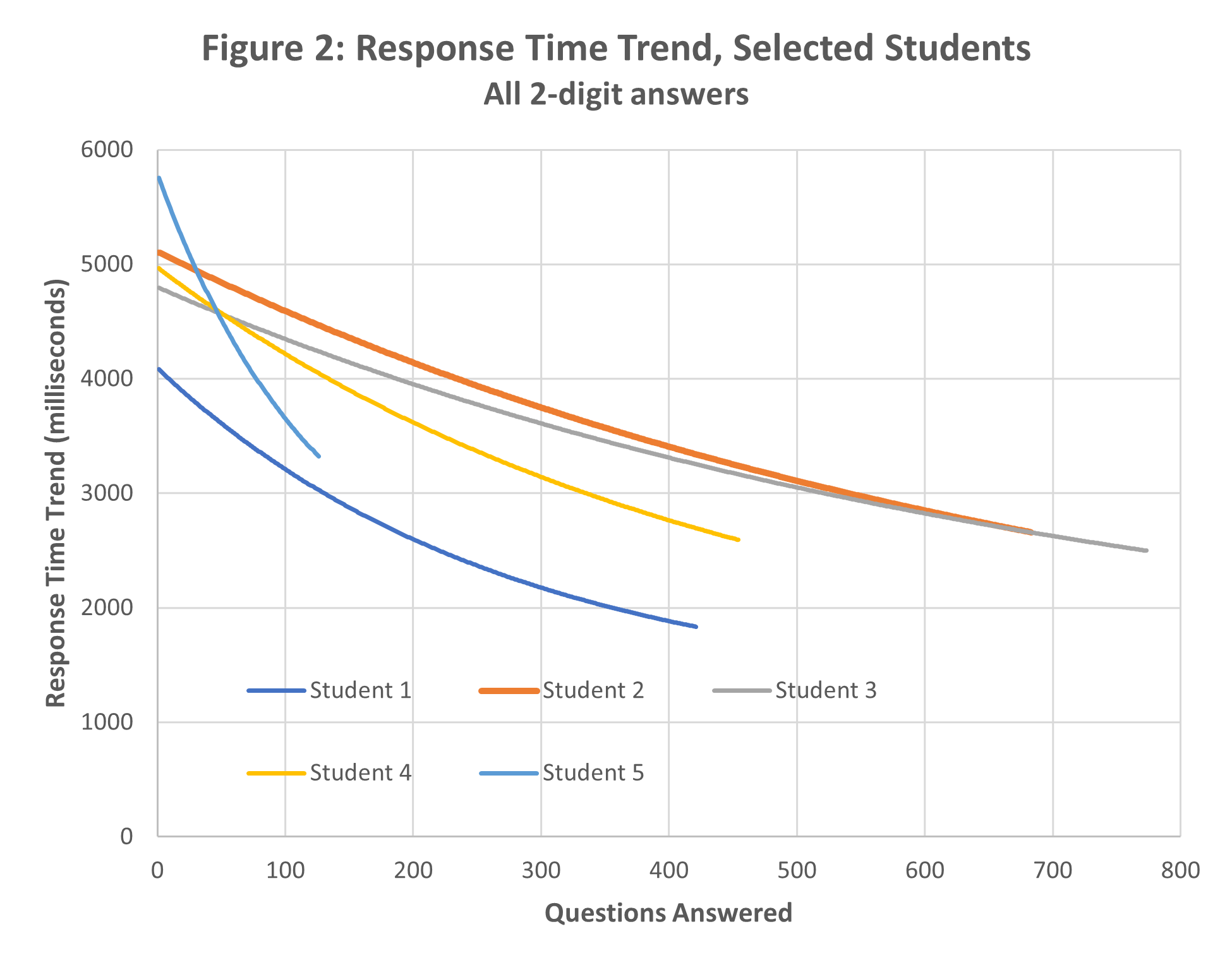
The exponential decay function in all cases predicted an asymptotic limit to response time between 1 and 1.5 seconds. As no student was performing close to this level, the estimates are likely to be inaccurate, but this will have little effect on the trendlines. Student gains appear to follow different trajectories, with estimates of the “half-life” approaching asymptotic limit ranging from 90 (student 5) to 503 questions (student 2 and student 3). That is the predicted effort required from any starting point to realise half of the potential speed gains. These predictions also have limited accuracy but do highlight that students learn at different rates. As we have discussed previously, individualised revision is a highly effective strategy to assist students at risk of falling behind.
A solid grounding in the fundamentals is a key pillar of success at maths. This requires revision and repetition to consolidate learning and achieve automaticity in the times tables and similar knowledge. The repetition can become boring for the student, particularly as time gains become smaller. Fortunately, the other design aspects of Maths Invaders address this issue by presenting mixed content, and through the engaging multi-player game, Space Rescue.
Combining a deep understanding of learning theory and classroom practice with innovative technology is at the heart of EdAlive’s suite of online learning websites, and our research ensures that our products deliver the best and continue to improve.
EdAlive’s other online learning websites all incorporate equivalent technology – Typing Tournament, Words Rock, Baggin’ the Dragon Maths, Volcanic Panic Reading Success. Research indicates that students using these websites are also making remarkable learning progress.

References
Cholmsky, P. (2011). From acquisition to automaticity: The Reflex solution for math fact mastery. https://harringtonmath.com/wp-content/uploads/2012/01/Reflex_White_Paper.pdf
Jamshidifarsani, H., Tamayo-Serrano, P., Garbaya, S., Lim, T. (2021). “A three-step model for the gamification of training and automaticity acquisition.” Journal of Computer Assisted Learning, 37: 994-1014.